Bondi–Hoyle–Lyttleton accretion: Difference between revisions

Model for the accretion of a uniform gas by a massive body

Bondi–Hoyle–Lyttleton (BHL) accretion (also known as Bondi–Hoyle accretion) is a mathematical model for the accretion of a uniform gas by a massive body. It is a general model of accretion with multiple applications, such as accretion of the interstellar medium by neutron stars and black holes, or wind mass transfer in binary star systems.

It is named after Hermann Bondi, Fred Hoyle, and Raymond Lyttleton.

The accretion rate (in terms of rate of change of mass) of the BHL formalism is given by^[1]

M ˙ = α 2 π ( G M ) 2 ρ ( v 2 + c 2 ) 3 / 2 , {\displaystyle {\dot {M}}=\alpha {\frac {2\pi (GM)^{2}\rho }{(v^{2}+c^{2})^{3/2}}},}

where

Hoyle–Lyttleton accretion is a simplified^[a] version of BHL accretion which treats the gas as being supersonic.^[2]

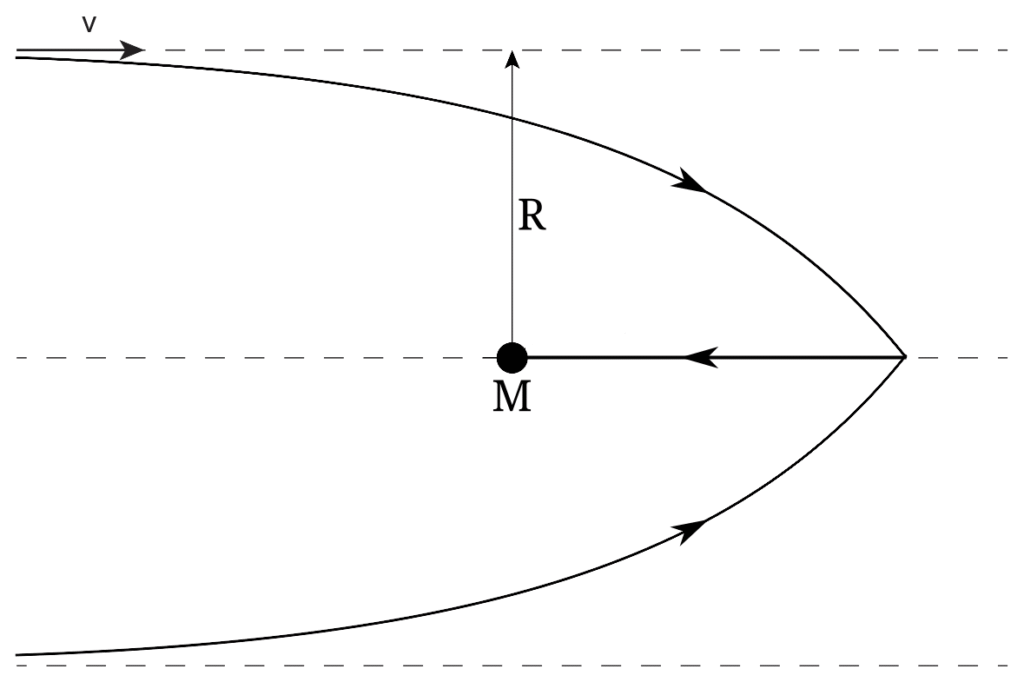
Hoyle–Lyttleton accretion assumes a homogeneous flow of incoming particles traveling with a (supersonic) velocity v {\displaystyle v} with density ρ {\displaystyle \rho } towards an accreting body with mass M {\displaystyle M} . The particles flow around the massive body, by which they are deflected towards the accretion line that lies behind it. At the accretion line, the particles collide, which cancels their momenta in the radial direction.

Depending on the initial velocity v {\displaystyle v} and the radial distance from the massive body R {\displaystyle R} , a particle may either be gravitationally bound to the body or not. A bound particle will then be accreted, while an unbound particle will escape. The initial velocity needed to escape from the massive body is given by its escape velocity at the distance R {\displaystyle R} . Thus, the condition for a particle to be accreted is

v < 2 G M R . {\displaystyle v<{\sqrt {\frac {2GM}{R}}}.}

This equation can also be written in terms of an accretion radius R acc {\displaystyle R_{\text{acc}}} . Thus, all particles that pass through a circle of this radius R acc {\displaystyle R_{\text{acc}}} around the massive body are accreted. This gives an accretion rate of

M ˙ = π ρ v R acc 2 = 4 π ( G M ) 2 ρ v 3 . {\displaystyle {\dot {M}}=\pi \rho vR_{\text{acc}}^{2}={\frac {4\pi (GM)^{2}\rho }{v^{3}}}.}

When taking into account some limited pressure effects and combining the resulting formula with Bondi accretion through an interpolation formula, the canonical formula for the BHL accretion rate can be found.

BHL accretion is used to model mass transfer in binary star systems, such as barium stars. For this, the velocity of the incoming flow is set to the relative velocity between the stellar wind and the accreting star (whose mass is M acc {\displaystyle M_{\text{acc}}} ) around the donating star (whose mass is M donor {\displaystyle M_{\text{donor}}} ), which is thus given by

v = v w 2 + v orb 2 , {\displaystyle v={\sqrt {v_{w}^{2}+v_{\text{orb}}^{2}}},}

where

• v w {\displaystyle v_{w}} is the velocity of the stellar wind;
• v orb = G M donor + M acc a {\displaystyle v_{\text{orb}}={\sqrt {G{\frac {M_{\text{donor}}+M_{\text{acc}}}{a}}}}} is the mean orbital velocity, where a {\displaystyle a} is the semimajor axis of the orbit.

Assuming that the stellar wind is emitted in a spherically symmetric way, it can be described by

M ˙ donor = 4 π v w ρ ( r ) r 2 , {\displaystyle {\dot {M}}_{\text{donor}}=4\pi v_{w}\rho (r)r^{2},}

where r {\displaystyle r} is the distance from the donor star.
Substituting these relations into the equation for the accretion rate, the accreted mass (per unit time) is given by

M ˙ acc = − a 1 2 a 2 1 − e 2 [ G M acc v w ] 2 [ 1 1 + ( v orb v w ) 2 ] 3 / 2 M ˙ donor , {\displaystyle {\dot {M}}_{\text{acc}}=-a{\frac {1}{2a^{2}{\sqrt {1-e^{2}}}}}\left[{\frac {GM_{\text{acc}}}{v_{w}}}\right]^{2}\left[{\frac {1}{1+({\frac {v_{\text{orb}}}{v_{w}}})^{2}}}\right]^{3/2}{\dot {M}}_{\text{donor}},}

where e {\displaystyle e} is the eccentricity of the orbit and where the r 2 {\displaystyle r^{2}} was replaced by its average value a 2 1 − e 2 {\displaystyle a^{2}{\sqrt {1-e^{2}}}} during the orbit^[1].