| 2 || K<sub>2</sub>||[[File:1-simplex t0.svg|60px]] || 1 || 1 || (2₁ 1₂) || 2K<sub>1</sub>|| || 0 || 0 || 2|| [https://www.weddslist.com/rmdb/1graph.php?gr=k2 WL]
| 2 || K<sub>2</sub>||[[File:1-simplex t0.svg|60px]] || 1 || 1 || (2₁ 1₂) || 2K<sub>1</sub>|| || 0 || 0 || 2|| [https://www.weddslist.com/rmdb/1graph.php?gr=k2 WL]
|-
|-
| 3 || K<sub>3</sub><BR>[[Triangle]]||[[File:2-simplex t0.svg|60px]] || 3 || 2 || (3₂ 3₂) || 3K<sub>1</sub>|| || 0 || 0 || 6|| [https://www.weddslist.com/rmdb/1graph.php?gr=k3 WL] [https://mathworld.wolfram.com/TriangleGraph.html MW]
| 3 || K<sub>3</sub><BR>[[Triangle]]||[[File:2-simplex t0.svg|60px]] || 3 || 2 || (3₂ 3₂) || 3K<sub>1</sub>|| || 0 || 0 || 6|| [https://www.weddslist.com/rmdb/1graph.php?gr=k3 WL] [https://mathworld.wolfram.com/TriangleGraph.html MW]
|- style=”background-color:#ffffc0″
|- style=”background-color:#ffffc0″
| 4 || K<sub>4</sub><BR>[[N-skeleton|Sk<sub>1</sub>]] [[tetrahedron]]||[[File:3-simplex t0.svg|60px]] || 6 || 3 || (4₃ 6₂) || 4K<sub>1</sub>|| || || || 24|| [https://www.weddslist.com/rmdb/1graph.php?gr=k4 WL] [https://mathworld.wolfram.com/TetrahedralGraph.html MW]
| 4 || K<sub>4</sub><BR>[[N-skeleton|Sk<sub>1</sub>]] [[tetrahedron]]||[[File:3-simplex t0.svg|60px]] || 6 || 3 || (4₃ 6₂) || 4K<sub>1</sub>|| || || || 24|| [https://www.weddslist.com/rmdb/1graph.php?gr=k4 WL] [https://mathworld.wolfram.com/TetrahedralGraph.html MW]
|- style=”background-color:#ffffc0″
|- style=”background-color:#ffffc0″
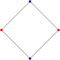
| 4 || C<sub>4</sub><BR>[[square]]||[[File:Regular_polygon_4_annotated.svg|60px]] || 4 || 2 || (4₂ 4₂) || 2K<sub>2</sub>||[[File:Regular star figure 2(2,1).svg|60px]] || 2 || 1 || 8|| [https://www.weddslist.com/rmdb/1graph.php?gr=c4 WL] [https://mathworld.wolfram.com/SquareGraph.html MW]
| 4 || C<sub>4</sub><BR>[[square]]||[[File:Regular_polygon_4_annotated.svg|60px]] || 4 || 2 || (4₂ 4₂) || 2K<sub>2</sub>||[[File:Regular star figure 2(2,1).svg|60px]] || 2 || 1 || 8|| [https://www.weddslist.com/rmdb/1graph.php?gr=c4 WL] [https://mathworld.wolfram.com/SquareGraph.html MW]
|-
|-
| 5 || K<sub>5</sub><BR>[[N-skeleton|Sk<sub>1</sub>]] [[5-cell]]||[[File:4-simplex t0.svg|60px]] || 10 || 4 || (5₄ 10₂) || 5K<sub>1</sub>|| || 0 || 0 || 120|| [https://www.weddslist.com/rmdb/1graph.php?gr=k5 WL] [https://mathworld.wolfram.com/PentatopeGraph.html MW]
| 5 || K<sub>5</sub><BR>[[N-skeleton|Sk<sub>1</sub>]] [[5-cell]]||[[File:4-simplex t0.svg|60px]] || 10 || 4 || (5₄ 10₂) || 5K<sub>1</sub>|| || 0 || 0 || 120|| [https://www.weddslist.com/rmdb/1graph.php?gr=k5 WL] [https://mathworld.wolfram.com/PentatopeGraph.html MW]
|-
|-
| 5 || C<sub>5<sub><BR>[[pentagon]]||[[File:Regular_polygon_5_annotated.svg|60px]][[File:Regular star polygon 5-2.svg|60px]] || 5 || 2 || (5₂ 5₂) || || || || || 10|| [https://www.weddslist.com/rmdb/1graph.php?gr=c5 WL] [https://mathworld.wolfram.com/CycleGraph.html MW]
| 5 || C<sub>5<sub><BR>[[pentagon]]||[[File:Regular_polygon_5_annotated.svg|60px]][[File:Regular star polygon 5-2.svg|60px]] || 5 || 2 || (5₂ 5₂) || || || || || 10|| [https://www.weddslist.com/rmdb/1graph.php?gr=c5 WL] [https://mathworld.wolfram.com/CycleGraph.html MW]
|- style=”background-color:#ffffc0″
|- style=”background-color:#ffffc0″
| 6 || K<sub>6</sub><BR>[[N-skeleton|Sk<sub>1</sub>]][[5-simplex]]||[[File:5-simplex t0.svg|60px]] || 15 || 5 || (6₅ 15₂) || 6K<sub>1</sub>|| || 0 || 0 || 720|| [https://www.weddslist.com/rmdb/1graph.php?gr=k6 WL]
| 6 || K<sub>6</sub><BR>[[N-skeleton|Sk<sub>1</sub>]][[5-simplex]]||[[File:5-simplex t0.svg|60px]] || 15 || 5 || (6₅ 15₂) || 6K<sub>1</sub>|| || 0 || 0 || 720|| [https://www.weddslist.com/rmdb/1graph.php?gr=k6 WL]
|- style=”background-color:#ffffc0″
|- style=”background-color:#ffffc0″
| 6 || K<sub>2,2,2</sub><BR>[[N-skeleton|Sk<sub>1</sub>]] [[octahedron]]||[[File:Complex tripartite graph octahedron.svg|60px]] || 12 || 4 || (6₄ 12₂) || 3K<sub>2</sub>||[[File:Regular star figure 3(2,1).svg|60px]] || 3 || 1 || 48|| [https://www.weddslist.com/rmdb/1graph.php?gr=k2,2,2 WL] [https://mathworld.wolfram.com/OctahedralGraph.html MW]
| 6 || K<sub>2,2,2</sub><BR>[[N-skeleton|Sk<sub>1</sub>]] [[octahedron]]||[[File:Complex tripartite graph octahedron.svg|60px]] || 12 || 4 || (6₄ 12₂) || 3K<sub>2</sub>||[[File:Regular star figure 3(2,1).svg|60px]] || 3 || 1 || 48|| [https://www.weddslist.com/rmdb/1graph.php?gr=k2,2,2 WL] [https://mathworld.wolfram.com/OctahedralGraph.html MW]
A symmetric graph (arc-transitive graph) is a graph that is both vertex transitive and edge transitive.
Key
- Cn is Cyclic graph.
- Kn is Complete graph.
- Kn,n is Complete bipartite graph.
- Complement of Kn,n is 2Kn.
- Kn,n,… is multipartite graph.
- Complement of Kn,…,n (m-partite) is mKn.
- nG is unconnected set of n G graphs.
- nG is n unconnected graphs G, aut(nG) is n! aut(G)n.
- × is tensor product of graphs (Kronecker product).
- G × K2 is called a bipartite double cover, making 2 copies of G if G is already bipartite.
- Cn × K2 = 2Cn, n even (bipartite)
- Cn × K2 = C2n, n odd (not bipartite)
- G(n,k) is generalized Petersen graph, cubic symmetric for (4,1), (5,2), (8,3), (10,2), (10,3), (12,5), (24,5).
- G(4,1) is skeleton of a cube, (8,12).
- G(5,2) is Petersen graph, (10,15).
- G(8,3) is Möbius–Kantor graph, (16,24).
- G(10,2) is Dodecahedral graph, (20,30).
- G(10,3) is Desargues graph, (20,30).
- G(12,5) is Nauru graph, (24,36).
Families
| Bipartite | Tripartite | 4-partite | 5-partite | 6-partite | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| K2,2 | K3,3 | K4,4 | K5,5 | K6,6 | K2,2,2 | K3,3,3 | K4,4,4 | K2,2,2,2 | K3,3,3,3 | K2,2,2,2,2 | K2,2,2,2,2,2 |

|

|

|

|

|

|

|

|

|

|

|

|
List
| v | Graph | Complement graph | Aut | Src | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | Graph | Edges | Degree | Configuration | Name | Graph | Edges | Degree | |||
| 2 | K2 |  |
1 | 1 | (2₁ 1₂) | 2K1 | 0 | 0 | 2 | WL | |
| 3 | K3 Triangle |
 |
3 | 2 | (3₂ 3₂) | 3K1 |  |
0 | 0 | 6 | WL MW |
| 4 | K4 Sk1 tetrahedron |
 |
6 | 3 | (4₃ 6₂) | 4K1 |  |
0 | 0 | 24 | WL MW |
| 4 | C4 square |
 |
4 | 2 | (4₂ 4₂) | 2K2 |  |
2 | 1 | 8 | WL MW |
| 5 | K5 Sk1 5-cell |
 |
10 | 4 | (5₄ 10₂) | 5K1 |  |
0 | 0 | 120 | WL MW |
| 5 | C5 pentagon |
  |
5 | 2 | (5₂ 5₂) | 10 | WL MW | ||||
| 6 | K6 Sk15-simplex |
 |
15 | 5 | (6₅ 15₂) | 6K1 |  |
0 | 0 | 720 | WL |
| 6 | K2,2,2 Sk1 octahedron |
 |
12 | 4 | (6₄ 12₂) | 3K2 |  |
3 | 1 | 48 | WL MW |
| 6 | K3,3 |  |
9 | 3 | (6₃ 9₂) | 2K3 |  |
6 | 2 | 72 | WL MW |
| 6 | C6 hexagon |
 |
6 | 2 | (6₂ 6₂) | 0 | 12 | WL | |||
| 7 | K7 Sk1 6-simplex |
 |
21 | 6 | (7₆ 21₂) | 7K1 | 0 | 0 | 5040 | WL | |
| 7 | C7 heptagon |
   |
7 | 2 | (7₂ 7₂) | 14 | WL MW | ||||
| 8 | K8 Sk17-simplex |
 |
28 | 7 | (8₇ 28₂) | 8K1 | 0 | 0 | 40320 | WL | |
| 8 | K2,2,2,2 Sk1 16-cell |
 |
24 | 6 | (8₆ 24₂) | 4K2 |  |
4 | 1 | 384 | WL MW |
| 8 | 2C4 |  |
8 | 2 | 128 | ||||||
| 8 | K4,4 Ci₈(1,3) |
 |
16 | 4 | (8₄ 16₂) | 2K4 | 12 | 3 | 1152 | WL MW | |
| 8 | Q3= G(4,1) = K4×K2 Sk1 cube |
 |
12 | 3 | (8₃ 12₂) | 48 | WL MW | ||||
| 8 | C8 octagon |
  |
8 | 2 | (8₂ 8₂) | 16 | WL MW | ||||
| 9 | K9 Sk1 8-simplex |
 |
36 | 8 | (9₈ 36₂) | 9K1 | 0 | 0 | 362880 | WL | |
| 9 | K3,3,3 |  |
27 | 6 | (9₆ 27₂) | 3K3 |  |
9 | 2 | 1296 | WL |
| 9 | K3×K3Sk1 3-3 duoprism |  |
18 | 4 | (9₄ 18₂) | 72 | WL | ||||
| 9 | C9 Enneagon |
 |
9 | 2 | (9₂ 9₂) | 18 | WL MW | ||||
| 10 | K10 Sk1 9-simplex |
 |
45 | 9 | (10₉ 45₂) | 10K1 | 0 | 0 | 3628800 | ||
| 10 | K5×K2 Ci10(1,4) |
 |
20 | 4 | (10₄ 20₂) | 240 | WL MW | ||||
| 10 | K2,2,2,2,2 Sk1 5-orthoplex |
 |
40 | 8 | (10₈ 40₂) | 5K2 |  |
5 | 1 | 3840 | |
| 10 | 2C5 |  |
10 | 2 | 200 | ||||||
| 10 | K5,5 |  |
25 | 5 | (10₅ 25₂) | 2K5 | 20 | 4 | 28800 | WL MW | |
| 10 | G(5,2) |  |
15 | 3 | (10₃ 15₂) | 120 | WL MW | ||||
| 10 | C10 pentagon |
  |
10 | 2 | (10₂ 10₂) | 20 | WL MW | ||||
| 11 | K11 Sk1 10-simplex Sk1 11-cell |
 |
55 | 10 | (11₁₀ 55₂) | 11K1 | 0 | 0 | 39916800 | ||
| 11 | C11 henagon |
11 | 2 | (11₂ 11₂) | 22 | WL MW | |||||
| 12 | K12 Sk1 11-simplex |
 |
66 | 11 | (12₁₁ 66₂) | 12K1 | 0 | 0 | 479001600 | ||
| 12 | K2,2,2,2,2,2 Sk1 6-orthoplex |
 |
60 | 10 | (12₁₀ 60₂) | 6K2 |  |
6 | 1 | 46080 | WL |
| 12 | 2C6 |  |
12 | 2 | 288 | ||||||
| 12 | 3C4 |  |
12 | 2 | 3072 | ||||||
| 12 | K3,3,3,3 |  |
54 | 9 | (12₉ 54₂) | 4K3 |  |
12 | 2 | 31104 | WL |
| 12 | K4,4,4 |  |
48 | 8 | (12₈ 48₂) | 3K4 | 18 | 3 | 82944 | WL | |
| 12 | 2K3,3 | 18 | 3 | 10368 | |||||||
| 12 | 2K2,2,2 | 24 | 4 | 4608 | |||||||
| 12 | K6,6 |  |
36 | 6 | (12₆ 36₂) | 2K6 | 30 | 5 | 1036800 | WL MW | |
| 12 | K4×K3 |  |
36 | 6 | (12₆ 36₂) | 144 | |||||
| 12 | K6×K2 |  |
30 | 5 | (12₅ 30₂) | 1440 | WL MW | ||||
| 12 | Sk1 icosahedron |  |
30 | 5 | (12₅ 30₂) | 120 | WL | ||||
| 12 | K2,2,2×K2 = C4×K3 |
 |
24 | 4 | (12₄ 24₂) | 768 | WL | ||||
| 12 | Sk1 (cuboctahedron) |  |
24 | 4 | (12₄ 24₂) | 48 | WL | ||||
| 12 | C12 |   |
12 | 2 | (12₂ 12₂) | 24 | WL MW | ||||
See also
References
- Handbook of Product Graphs, 2nd ed. Hammack, R.; Imrich, W.; and Klavžar, S., Boca Raton, FL: CRC Press, 2016.
- Symmetric graphs index <50v … I have all, and extra 8, K10…
- Classification of tensor products of symmetric graphs Wilfried Imrich, Ales Pultr, 1991
- Weisstein, Eric W. “Cubic symmetric graphs”. MathWorld.
- Weisstein, Eric W. “Quartic symmetric graphs”. MathWorld.
- Weisstein, Eric W. “Circulant Graph”. MathWorld.